https://doi.org/10.1140/epjp/s13360-020-00579-2
Regular Article
Solving procedure for the motion of infinitesimal mass in BiER4BP
1
Plekhanov Russian University of Economics, Scopus number 60030998, Moscow, Russia
2
Sternberg Astronomical Institute, M.V. Lomonosov’s Moscow State University, 13 Universitetskij prospect, 119992, Moscow, Russia
3
Odessa State Academy of Civil Engineering and Architecture, Odessa, Ukraine
4
Odessa I. I. Mechnikov National University, 2 Dvoryanskaya St., Odessa, Ukraine
Received:
8
May
2020
Accepted:
29
June
2020
Published online:
27
July
2020
In this paper, we present a new ansatz for solving equations of motion for the trapped orbits of the infinitesimal mass m, which is moving near the primary M3 in case of bi-elliptic restricted problem of four bodies (BiER4BP), where three primaries M1, M2, M3 are rotating around their common center of mass on elliptic orbits with hierarchical configuration M3 ≪ M2 ≪ M1. A new type of the solving procedure is implemented here to obtain the coordinates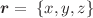 
of the infinitesimal mass m with its orbit located near the primary M3. Meanwhile, the system of equations of motion has been successfully explored with respect to the existence of analytical or semi-analytical (approximated) way for presentation of the solution. We obtain as follows: (1) the solution for coordinate x is described by the key nonlinear ordinary differential equation of fourth order at simplifying assumptions, (2) solution for coordinate y is given by the proper analytical expression, depending on coordinate x and true anomaly f, (3) the expression for coordinate z is given by the equation of Riccati-type—it means that coordinate z should be quasi-periodically oscillating close to the fixed plane 
.
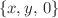© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2020
