https://doi.org/10.1140/epjp/s13360-020-00204-2
Regular Article
Bilinear form, solitons, breathers and lumps of a (3 + 1)-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt equation in ocean dynamics, fluid mechanics and plasma physics
Ministry-of-Education Key Laboratory of Fluid Mechanics and National Laboratory for Computational Fluid Dynamics, Beijing University of Aeronautics and Astronautics, 100191, Beijing, China
Received:
4
August
2019
Accepted:
11
November
2019
Published online:
27
February
2020
A 
-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt equation in ocean dynamics, fluid mechanics and plasma physics is investigated in this paper. Bilinear form, soliton and breather solutions are derived via the Hirota method. Lump solutions are also obtained. Amplitudes of the solitons are proportional to the coefficient 
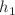, while inversely proportional to the coefficient 
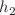. Velocities of the solitons are proportional to the coefficients , 
, 
, 
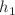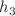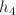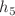and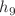 
. Elastic and inelastic interactions between the solitons are graphically illustrated. Based on the two-soliton solutions, breathers and periodic line waves are presented. We find that the lumps propagate along the straight lines affected by 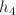and 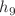. Both the amplitudes of the hump and valleys of the lump are proportional to 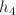, while inversely proportional to 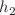. It is also revealed that the amplitude of the hump of the lump is eight times as large as the amplitudes of the valleys of the lump. Graphical investigation indicates that the lump which consists of one hump and two valleys is localized in all directions and propagates stably.
© Società Italiana di Fisica (SIF) and Springer-Verlag GmbH Germany, part of Springer Nature 2020
