https://doi.org/10.1140/epjp/s13360-020-00126-z
Regular Article
Excited states of odd-mass nuclei with different deformation-dependent mass coefficients
1
High Energy Physics and Astrophysics Laboratory, Department of Physics, Faculty of Sciences Semlalia, Cadi Ayyad University, P.O.B. 2390, 40000, Marrakesh, Morocco
2
ESMaR, Department of Physics, Faculty of Sciences, Mohammed V University, Rabat, Morocco
* e-mail: oulne@uca.ma
Received:
19
September
2019
Accepted:
3
December
2019
Published online:
3
February
2020
Some experimental data indicate that the mass tensor of collective Bohr Hamiltonian should be considered as a function of the collective coordinates rather than a constant (Bonatsos et al. in Phys Rev C 83:044321, 2011). In this work, our purpose is to investigate the properties of low-lying collective states of the odd nuclei 
Yb and 
Dy by using a new generalized version of the collective quadrupole Bohr Hamiltonian with deformation-dependent mass coefficients. The proposed new version of the Bohr Hamiltonian is solved for Davidson potential in 
shape variable, while the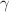 
potential is taken to be equal to the harmonic oscillator. The obtained results of the excitation energies and B(E2) reduced transition probabilities show an overall agreement with the experimental data. Moreover, we investigate the effect of the deformation-dependent mass parameter on energy spectra and transition rates in both cases, namely when the mass coefficients are different and when they are equal. Besides, we will show the positive effect of the present formalism on the moment of inertia.
© Società Italiana di Fisica (SIF) and Springer-Verlag GmbH Germany, part of Springer Nature, 2020
