https://doi.org/10.1140/epjp/i2019-12506-5
Regular Article
Description of critical point nuclei within an energy-dependent geometric model
1
Horia Hulubei National Institute of Physics and Nuclear Engineering, RO-077125, Bucharest-Magurele, Romania
2
Academy of Romanian Scientists, 54 Splaiul Independenţei, RO-050094, Bucharest, Romania
* e-mail: rbudaca@theory.nipne.ro
Received:
26
September
2018
Accepted:
10
January
2019
Published online:
12
April
2019
An exactly solvable version of the Bohr Hamiltonian is proposed for a unified treatment of transitional nuclei. The model employs an energy-dependent potential in the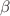 
shape variable which is amended with a centrifugal contribution from the 
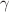and angular degrees of freedom. The parametrization of the 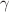part of the potential enables the connection between the adiabatic separation of 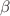and 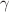fluctuations suitable for critical point nuclei and the exactly separable solutions specific to deformed nuclei. The fully analytical model is applied to known critical point nuclei as well as a neighbouring isotope for each case. Beside very good agreement with experiment for energies and electromagnetic transitions, numerical results also reveal specific model characteristics for critical nuclei in comparison to more or less deformed nuclei.
© Società Italiana di Fisica / Springer-Verlag GmbH Germany, part of Springer Nature, 2019
