Eur. Phys. J. Plus (2019) 134: 562
https://doi.org/10.1140/epjp/i2019-12980-7

Regular Article

Exact solutions of a nonpolynomial oscillator related to isotonic oscillator

¹ Laboratorio de Información Cuántica, CIDETEC, Instituto Politécnico Nacional, UPALM, CDMX, 07700, Mexico City, Mexico
² Catedrática CONACYT, CIC, Instituto Politécnico Nacional, CDMX 07700, Mexico City, Mexico
³ Department of Mathematics and Statistics, University of Prince Edward Island, 550 University Avenue, C1A 4P3, Charlottetown, PEI, Canada

^* e-mail: dongsh2@yahoo.com

Received: 21 June 2019
Accepted: 1 September 2019
Published online: 12 November 2019

Abstract

We find that the analytical solutions to a quantum system with a nonpolynomial oscillator potential related to isotonic oscillator are given by the confluent Heun functions 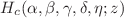. The properties of the wave functions, which are strongly relevant for the potential parameters a and g, are illustrated. It is shown that the wave functions are shrunk to the origin for a given a when the potential parameter g increases, while the wave peak of wave functions is concaved to the origin when the negative potential parameter 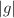increases. Moreover, the wave peaks of the even wave functions become sharper when the potential parameter decreases, but they become flat when the potential parameter increases. When the minimum value tends to zero, this nonpolynomial oscillator reduces to a harmonic oscillator.