A direct discontinuous Galerkin method for fractional convection-diffusion and Schrödinger-type equations

Tarek Aboelenen

doi:10.1140/epjp/i2018-12166-y

EPJ

a
b
c
d
e
ap
st
h
plus
ds
pv
ti
qt
am
n

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Eur. Phys. J. Plus (2018) 133: 316
https://doi.org/10.1140/epjp/i2018-12166-y

Regular Article

A direct discontinuous Galerkin method for fractional convection-diffusion and Schrödinger-type equations

Tarek Aboelenen^*

Department of Mathematics, Assiut University, 71516, Assiut, Egypt

^* e-mail: tarek.aboelenen@aun.edu.eg

Received: 6 May 2018
Accepted: 29 June 2018
Published online: 9 August 2018

Abstract

A direct discontinuous Galerkin (DDG) finite element method is developed for solving fractional convection-diffusion and Schrödinger-type equations with a fractional Laplacian operator of order 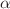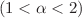$\alpha$ $(1 < \alpha < 2)$ . The fractional operator of order 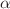$\alpha$ is expressed as a composite of second-order derivative and a fractional integral of order $2-\alpha$ . These problems have been expressed as a system of parabolic equations and low-order integral equation. 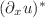This allows us to apply the DDG method, which is based on the direct weak formulation for solutions of fractional convection-diffusion and Schrödinger-type equations in each computational cell, letting cells communicate via the numerical flux $(\partial_{x}u)^{\ast}$ only. Moreover, we prove stability and optimal order of convergence 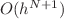$O(h^{N+1})$ for the general fractional convection-diffusion and Schrödinger problems, where h, N are the space step size and polynomial degree. The DDG method has the advantage of easier formulation and implementation as well as the high-order accuracy. Finally, numerical experiments confirm the theoretical results of the method.