https://doi.org/10.1140/epjp/i2018-12119-6
Regular Article
Stability analysis of nonlinear fractional differential equations with Caputo and Riemann-Liouville derivatives
1
Department of Mathematics, University of Peshawar, P.O. Box 25000, Khybar Pakhtunkhwa, Pakistan
2
UAE University, Department of Mathematical Sciences, College of Science, P.O. Box 17551, Al-Ain, United Arab Emirates
3
State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Hohai University, 210098, 210098, Nanjing, China
4
Shaheed Benazir Bhutto University, Sheringal, 18000, Dir Upper, Khyber Pakhtunkhwa, Pakistan
* e-mail: m.syam@uaeu.ac.ae
Received:
7
May
2018
Accepted:
28
May
2018
Published online:
20
July
2018
In this paper, we study the existence and uniqueness of solutions for nonlinear fractional differential equations with Caputo and Riemann-Liouville derivatives, and p -Laplacian operator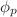 
based on the Banach contraction principle. Also, we investigate the stability results for the proposed problem. Appropriate example is given to demonstrate the established results.
© Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature, 2018
