https://doi.org/10.1140/epjp/s13360-025-06624-2
Regular Article
Logistic models inspired by non-Gaussian statistics: an application to tumor growth
1
Department of Physics, State University of Rio Grande do Norte, 59610-210, Mossoró, RN, Brasil
2
Department of Plant Science, Federal Rural University of the Semi-Arid, 59625-900, Mossoró, RN, Brasil
Received:
27
May
2025
Accepted:
4
July
2025
Published online:
9
July
2025
Fully understanding how cancer tumors evolve remains a complex challenge. Due to this, several mathematical models of tumor growth have been proposed over the past decade, with logistic models standing out. This paper presents generalized logistic models based on the deformed algebras of Tsallis and Kaniadakis. The proposed models describe tumor growth dynamics within the framework of non-Gaussian statistics. As alternatives to traditional Gompertz and Verhulst models, the 
Gompertz, Verhulst,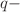 
Gompertz, and 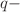Verhulst models are introduced. These new models offer greater flexibility in capturing diverse tumor growth patterns, which may be useful in cases where conventional models have limitations. To assess their validity, we analyze a tumor growth dataset compiled from eight separate trials, totaling 581 observations. Using a Bayesian model comparison based on the Bayes factor, our findings reveal that the 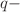Verhulst model best describes the examined dataset. In conclusion, this study provides new insights into tumor growth modeling, demonstrating how generalized statistical algebraic frameworks can enhance our understanding of complex biological processes.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
