Eur. Phys. J. Plus (2025) 140: 559
https://doi.org/10.1140/epjp/s13360-025-06485-9

Regular Article

Polynomial potentials and nilpotent groups

¹ Institute of Physics, University of Graz, Universitätsplatz 5, A-8010, Graz, Austria
² Department of Physics and Astronomy, University of Iowa, Iowa City, USA

^a wolfgang.schweiger@uni-graz.at

Received: 16 April 2025
Accepted: 26 May 2025
Published online: 20 June 2025

Abstract

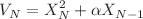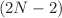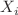This paper deals with the partial solution of the energy-eigenvalue problem for one-dimensional Schrödinger operators of the form $H_N=X_0^2+V_N$, where $V_N=X_N^2+\alpha X_{N-1}$ is a polynomial potential of degree $(2N-2)$ and $X_i$ are the generators of an irreducible representation of a particular nilpotent group 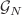${\mathcal{G}}_N$. Algebraization of the eigenvalue problem is achieved for eigenfunctions of the form 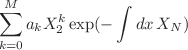${\sum }_{k=0}^M{a}_k{X}_2^{k}exp(-\int dx{X}_N)$. 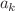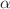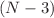It is shown that the overdetermined linear system of equations for the coefficients $a_k$ has a nontrivial solution, if the parameter $\alpha$ and $(N-3)$ Casimir invariants satisfy certain constraints. This general setting works for even 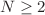$N\ge 2$ and can also be applied to odd 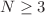$N\ge 3$, if the potential is symmetrized by considering it as function of |x| rather than x. It provides a unified approach to quasi-exactly solvable polynomial interactions, including the harmonic oscillator, and extends corresponding results known from the literature. Explicit expressions for energy eigenvalues and eigenfunctions are given for the quasi-exactly solvable sextic, octic and decatic potentials. The case of 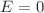$E=0$ solutions for general N and M is also discussed. As physical application, the movement of a charged particle in an electromagnetic field of pertinent polynomial form is shortly sketched.