https://doi.org/10.1140/epjp/s13360-025-06440-8
Regular Article
Quantum circuit theory by unitary operators derived from Kaniadakis κ-generalization
Federal University of Ceará—Itapajé Campus, 62600-000, Itapajé, Ceará, Brazil
Received:
10
December
2024
Accepted:
17
May
2025
Published online:
12
June
2025
Quantum gates are the basis for building circuits in Quantum Computing and are mathematically represented by unitary matrices. This work investigates the theory of unitary matrices related to Kaniadakis κ-generalized formalism. Initially a family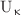 
of unitary operators for 
are obtained. Secondly, analytical quotas for the quantum circuit complexity for a unitary group 
are described using the κ-exponential and Lambert-Kaniadakis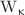 
functions. Lastly, a quantum circuit of an radial basis function network that uses the κ-gaussian function in its activation function is shown.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
