https://doi.org/10.1140/epjp/s13360-025-06315-y
Regular Article
Earthquake waves in a modified Burridge and Knopoff model
1
Department of Physics, Higher Teachers Training College of Bertoua, University of Bertoua, Bertoua, Cameroon
2
Department of Physics, Faculty of Science, University of Yaounde I, Yaounde, Cameroon
3
Department of Physics, Government High School Minkama, Ministry of Secondary Education, Obala, Cameroon
Received:
13
November
2024
Accepted:
10
April
2025
Published online:
30
May
2025
The propagation of nonlinear waves in a mass-spring system modelled by a modified Burridge and Knopoff model for earthquakes is studied. The spatio-temporal dynamics of the system is found by taking into account the hydrodynamic coupling damping forces, the stiffness of the elasticity of the rock material in a nonlinear form, and the empirical friction forces experimentally approved. The blocks are placed on a downward slope with an angle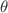 
with respect to the horizontal line. The theoretical framework for the analysis shows that the system can be reduced into two components: an oscillating part and a non-oscillating part. While the oscillating part is a nonlinear earthquake wave equation describing the behaviour of the earthquake waves propagating in the Earth crust, the non-oscillating part is a landslide equation describing the displacement of the ground during the shock. In the semi-discrete approximation, the nonlinear earthquake wave equation is shown to be governed by a dissipative bright-like soliton solution of the complex Ginzburg–Landau (CGL) equation, while the ground displacement equation is reduced to the residual displacement of the blocks observed after the ground shaking. The relationship between landslide and floor velocity is found, showing that whether there is a slope or not, any earthquake-induced ground displacement whose importance depends on the duration of the ground shaking and the angle slope. In the linear limits, the system is found governed by a dissipative plane wave solution of the complex linear Schrodinger (CLS) equation. Also, we found that the amplitude and frequency vibration of the earthquake wave decreases due to friction (as well as to stiffness of rock material), while the inverse effect is observed on the propagation area.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
