https://doi.org/10.1140/epjp/s13360-025-06188-1
Regular Article
Discovery of exact solitons to the fractional KP-MEW equation with stability analysis
1
Department of Mathematics, Faculty of Science and Information Technology, Al-Zaytoonah University of Jordon, 11733, Amman, Jordan
2
Department of Mathematics, College of Science, Taibah University, P.O.Box 344, 42353, Madinah, Saudi Arabia
3
Operational Research Center in Healthcare, Near East University, TRNC Mersin 10, 99138, Nicosia, Turkey
4
Department of Mathematics, College of Science, Korea University, 145 Anam-ro, Seongbuk-gu, 02841, Seoul, South Korea
5
Department of Technical Sciences, Western Caspian University, 1001, Baku, Azerbaijan
6
Neighbourhood of Akcaglan, Imarli Street, Number: 28/4, 26030, Eskisehir, Turkey
Received:
30
December
2024
Accepted:
1
March
2025
Published online:
19
April
2025
This research derives the new solitons for the fluid wave model, a nonlinear Kadomtsev–Petviashvili-modified equal width model along truncated M-fractional derivative. Our concerned model is utilized to explain the matter-wave pulses, waves in ferromagnetic media, and long wavelength water waves with frequency dispersion and faintly nonlinear reinstating forces, and others. To this end, we apply the modified extended direct algebraic and the improved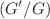 
-expansion techniques. Fractional transformation is utilized to convert the nonlinear fractional partial differential equation into a nonlinear ordinary differential equation. Mathematica software is used to gain the solutions, verify them, and demonstrate them in two-, three-dimensional, and contour plots. The impact of fractional derivative is represented through two-dimensional plot. A linear stability process is conducted to confirm that governing equation is stable. The techniques are reliable to use and provide the various types of solutions.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
