https://doi.org/10.1140/epjp/s13360-025-06170-x
Regular Article
Exploring data driven soliton and rogue waves in 
symmetric and spatio-temporal potentials using PINN and SC-PINN methods
1
Centre for Computational Modeling, Chennai Institute of Technology, 600069, Chennai, Tamil Nadu, India
2
Center for Nonlinear and Complex Networks, SRM TRP Engineering College, 621105, Tiruchirappalli, Tamil Nadu, India
3
Center for Research, SRM Institute of Science and Technology - Tiruchirappalli, 621105, Tiruchirappalli, Tamil Nadu, India
4
Department of General and Theoretical Physics, L. N. Gumilyov Eurasian National University, 010008, Astana, Kazakhstan
a manikandan.k@trp.srmtrichy.edu.in, manikandan.cnld@gmail.com
Received:
14
December
2024
Accepted:
22
February
2025
Published online:
12
March
2025
In this study, we present a deep learning (DL) framework for solving the nonlinear Schrödinger equation with -symmetric potentials using strongly constrained physics-informed neural networks (SC-PINNs). We focus on three types of physically compelling potentials, namely -symmetric rational, Jacobian-periodic, and spatio-temporal dependent. SC-PINNs extend the standard physics-informed neural networks (PINNs) by incorporating compound derivative information into the soft constraints, along with an adaptive weight mechanism to accelerate loss function convergence. This enhancement significantly improves the training efficiency compared to standard PINNs. We employ SC-PINNs to approximate soliton and rogue wave solutions of the system under investigation. Additionally, we uncover the impact of various factors on the neural network’s performance, including five different nonlinear activation functions: ReLU, sigmoid, sech, tanh, and sine. Our results reveal that the SC-PINNs method achieves faster convergence and lower errors compared to traditional PINNs. Notably, when using the sine activation function for the three distinct potentials mentioned above, SC-PINNs reduced errors to the order of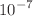 
, 
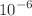, and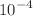 
, effectively capturing complex physical features for highly accurate predictions. Furthermore, we analyze the effect of -symmetric potential parameters on the obtained approximated solutions. The results demonstrate that our DL model successfully approximates soliton and rogue wave solutions of the considered system with high accuracy, outperforming traditional DL algorithms.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
