https://doi.org/10.1140/epjp/s13360-025-06151-0
Regular Article
Analytical and computational study of Fisher and Shannon information entropies in one and three-dimensional spaces for exponential-type potential
1
Theoretical Physics Group, Department of Physics, University of Uyo, Uyo, Akwa Ibom State, Nigeria
2
Physics Department, Bowen University, Iwo, Osun State, Nigeria
3
Department of Physics, Federal University of Technology, Ikot Abasi, Nigeria
4
Department of Basic Sciences, School of Intelligent Science and Engineering, Xi’an Peihua University, 710125, Xi’an, China
5
Department of Physics, University of Uyo, Uyo, Akwa Ibom State, Nigeria
6
Information Technology, Silver Oak College of Engineering Technology, Silver Oak University, 382481, Ahmedabad, Gujarat, India
7
Department of Mathematics, Instituto Federal Sudeste de Minas Gerais, Juiz de Fora-MG, Brazil
8
Theoretical and Computational Condensed Matter and Materials Physics Group, School of Chemistry and Physics, University of KwaZulu-Natal, Pietermaritzburg, South Africa
9
National Institute for Theoretical and Computational Sciences (NITheCS), KwaZulu-Natal, Durban, South Africa
10
Department of Physics, Akwa Ibom State University, Mkpat-Enin, Nigeria
11
Department of Physics, National Open University of Nigeria, Jabi, Abuja, Nigeria
12
Department of Physics, Faculty of Science, Modibbo Adamawa University, P. M.B, 2076, Nigeria
13
Department of Physics, Kogi State University, Anyigba, Kogi State, Nigeria
14
Physics Department, The Higher Canal Institute for Engineering and Technology, Suez Cairo, Egypt
15
Basic Science Department, The Higher technological institute, new Heliopolis, Cairo, Egypt
a ituenokon@uniuyo.edu.ng, ituenokonphysics@gmail.com
Received:
29
January
2025
Accepted:
18
February
2025
Published online:
25
March
2025
In this work, we study Fisher and Shannon information entropies for homonuclear hydrogen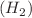 
and heteronuclear lithium hydride (LiH) molecules in one and three-dimensional spaces using exponential-type potential by solving Schrödinger wave equation with supersymmetric quantum mechanics approach. The momentum space wave function plots and their probability densities for both molecules at different quantum states are symmetrical and compacted with a unique pattern though both molecules showcase molecular localisation at different nodes of their respective quantum state. The numerical solutions obtained for both molecules satisfy the Bialynicki-Birula and Mycielski (BBM) inequalities for the different dimensions which authenticate the accuracy of both the analytical and computational solutions. The total normalised wave function used for the computation of information entropies for different dimensions was expressed as a hypergeometric function of the Jacobi polynomial.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
