https://doi.org/10.1140/epjp/s13360-025-06109-2
Regular Article
Scaling laws for optimal turbulent flow in tree-like networks with smooth and rough tubes and power-law fluids
1
Seminare Private Limited, 110059, Delhi, India
2
Punjab State Aeronautical Engineering College, Patiala, Punjab, India
3
Department of Chemical Engineering, Indian Institute of Technology Delhi, 110016, Delhi, India
a ashish.garg.iisc@gmail.com, ashish@seminare.in
Received:
19
June
2024
Accepted:
9
February
2025
Published online:
26
February
2025
In this paper, we establish optimized scaling laws for fully-developed turbulent flows of incompressible power-law fluids with index n within tree-like branching networks. Our analysis considers turbulence in both smooth and rough channels while accounting for constraints on the network’s volume and surface area. To characterize flow conditions, we introduce a dimensionless conductance parameter, E, and examine its dependence on the diameter ratio 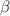 , branch splitting N, length ratio
, branch splitting N, length ratio  , and the number of branching generations m. The results indicate that E decreases as
, and the number of branching generations m. The results indicate that E decreases as  , N, and m increase, underscoring the impact of these factors on flow conductance. Furthermore, under volume constraints, we determine the optimal conditions for flow in both smooth and rough tube fractal networks, leading to distinct scaling relationships as
, N, and m increase, underscoring the impact of these factors on flow conductance. Furthermore, under volume constraints, we determine the optimal conditions for flow in both smooth and rough tube fractal networks, leading to distinct scaling relationships as  , and
, and 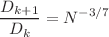 (or
(or  and
and 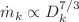 ), respectively, where
), respectively, where 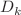 represents the tube diameter and
represents the tube diameter and 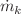 denotes the mass flow rate at the
denotes the mass flow rate at the 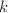 th branching level. Interestingly, in rough tube networks, the scaling behavior remains unaffected by the fluid index
th branching level. Interestingly, in rough tube networks, the scaling behavior remains unaffected by the fluid index 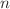 , whereas in smooth tube networks, it exhibits a dependence on
, whereas in smooth tube networks, it exhibits a dependence on 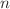 . Likewise, when constrained by surface area, the optimal flow conditions vary between smooth and rough tube networks, each following distinct scaling laws as
. Likewise, when constrained by surface area, the optimal flow conditions vary between smooth and rough tube networks, each following distinct scaling laws as 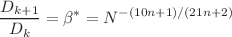 , and
, and 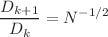 (or
(or  and
and 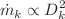 ), respectively. The smooth tube network once again exhibits dependence on the fluid index
), respectively. The smooth tube network once again exhibits dependence on the fluid index 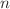 . Furthermore, our analysis reveals that in volume-constrained networks, the scaling exponent slope decreases as
. Furthermore, our analysis reveals that in volume-constrained networks, the scaling exponent slope decreases as 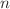 increases, whereas in surface-area-constrained networks, the trend is reversed. We find that the optimal flow condition aligns with the uniform distribution of pressure drop across each branching level within the network. This applies under both constraints for turbulent flow behavior in both smooth and rough-walled tubes. We validated our results against various previous theoretical predictions under limiting conditions. Additionally, this study explores the interplay between geometric and flow properties of parent and daughter tubes in branching networks. Furthermore, we also establish extended scaling-laws under optimal conditions, addressing critical parameters such as length ratios, average flow velocities, tube-volume, and surface-area within the fractal network. In summary, our research significantly extends the relevance of Murray’s Law in understanding and optimizing branching networks under diverse constraints and fluid characteristics. By addressing the interplay between non-Newtonian fluid behaviors and wall properties, our findings offer valuable strategies to enhance the performance and efficiency of engineering systems reliant on fluid dynamics.
increases, whereas in surface-area-constrained networks, the trend is reversed. We find that the optimal flow condition aligns with the uniform distribution of pressure drop across each branching level within the network. This applies under both constraints for turbulent flow behavior in both smooth and rough-walled tubes. We validated our results against various previous theoretical predictions under limiting conditions. Additionally, this study explores the interplay between geometric and flow properties of parent and daughter tubes in branching networks. Furthermore, we also establish extended scaling-laws under optimal conditions, addressing critical parameters such as length ratios, average flow velocities, tube-volume, and surface-area within the fractal network. In summary, our research significantly extends the relevance of Murray’s Law in understanding and optimizing branching networks under diverse constraints and fluid characteristics. By addressing the interplay between non-Newtonian fluid behaviors and wall properties, our findings offer valuable strategies to enhance the performance and efficiency of engineering systems reliant on fluid dynamics.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.




