https://doi.org/10.1140/epjp/s13360-025-06081-x
Regular Article
Stability, sensitivity, and bifurcation analysis of a fractional-order HIV model of CD
T cells with memory and external virus transmission from macrophages
1
Centre for Mathematical Biology and Ecology, Department of Mathematics, Jadavpur University, 188, Raja S.C. Mallick Road, 700032, Kolkata, India
2
Department of Mathematics, Mahadevananda Mahavidyalaya, 700120, Barrackpore, Kolkata, West Bengal, India
3
Department of Mathematics, South Asian University, Rajpur Road, Maidan Garhi, 110068, New Delhi, India
4
Centre for Mathematical and Financial Computing, Department of Mathematics, The LNM Institute of Information Technology, 302031, Jaipur, Rajasthan, India
Received:
27
October
2024
Accepted:
2
February
2025
Published online:
25
February
2025
This paper presents a fractional-order mathematical model in the Caputo sense to study the dynamics of HIV infection, focusing on the interactions among uninfected T cells, infected T cells, and HIV. The inclusion of fractional derivatives allows for the incorporation of memory effects, providing a more accurate representation of disease progression. We begin by establishing fundamental mathematical properties such as existence and uniqueness, positivity and boundedness of the solutions. The Caputo fractional derivative: Equilibrium points of the system are identified, and the basic reproduction number,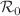 
, is calculated to assess the potential for infection spread. Sensitivity analysis of 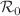is performed to determine the most influential parameters, both positively and negatively. The local and global stability analyses have been carried out for all equilibrium points. We also derive the transcritical and Hopf bifurcation conditions, revealing the onset of oscillatory behavior. Numerical simulations are carried out using the fractional forward Euler method, demonstrating how the fractional-order 
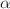significantly influences the disease dynamics. Our results indicate that higher values of 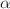are associated with oscillatory dynamics. In contrast, a reduction in 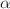contributes to the stabilization of the system, as evidenced by the bifurcation diagrams for various fractional orders. Additionally, we provide biological interpretations of all numerical results and compare every result with existing related models to highlight its novelty and relevance. The paper concludes with a summary of findings and potential future research directions.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
