https://doi.org/10.1140/epjp/s13360-025-06080-y
Regular Article
A gap between two approaches of dimensional reduction for a six-dimensional Kaluza–Klein theory
1
Phenikaa Institute for Advanced Study, Phenikaa University, 12116, Hanoi, Vietnam
2
Faculty of Basic Sciences, Phenikaa University, 12116, Hanoi, Vietnam
3
Institute of Physics, National Yang Ming Chiao Tung University, 30010, Hsin Chu, Taiwan
a
tuan.doquoc@phenikaa-uni.edu.vn
Received:
31
October
2024
Accepted:
1
February
2025
Published online:
22
February
2025
Inspired by the five-dimensional Kaluza–Klein theory, we would like to study the dimensional reduction issue of six-dimensional Kaluza–Klein extension in this paper. In particular, we will examine two possible approaches of dimensional reduction from six-dimensional spacetimes to four-dimensional ones. The first one is a direct dimensional reduction, i.e., from six-dimensional spacetimes directly to four-dimensional ones, via a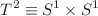 
compactification; while, the second one is an indirect dimensional reduction, i.e., from six-dimensional spacetimes to five-dimensional ones then four-dimensional ones, via two separated 
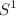compactifications. Interestingly, we show that these two approaches lead to different four-dimensional effective actions although using the same six-dimensional metric. It could therefore address an important question of which approach is more reliable than the other.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
