https://doi.org/10.1140/epjp/s13360-025-06067-9
Regular Article
Demkov–Fradkin tensor for curved harmonic oscillators
1
Department of Physics, Faculty of Science, Ankara University, 06100, Ankara, Türkiye
2
Departamento de Física Teórica, Atómica y Óptica, and IMUVA, Universidad de Valladolid, 47011, Valladolid, Spain
Received:
11
September
2024
Accepted:
28
January
2025
Published online:
20
February
2025
In this work, we obtain the Demkov–Fradkin tensor of symmetries for the quantum curved harmonic oscillator in a space with constant curvature given by a parameter 
. In order to construct this tensor, we have firstly found a set of basic operators which satisfy the following conditions: (i) Their products give symmetries of the problem; in fact, the Hamiltonian is a combination of such products; (ii) they generate the space of eigenfunctions as well as the eigenvalues in an algebraic way; (iii) in the limit of zero curvature, they come into the well-known creation/annihilation operators of the flat oscillator. The appropriate products of such basic operators will produce the curved Demkov–Fradkin tensor. However, these basic operators do not satisfy Heisenberg commutators but close another Lie algebra which depends on . As a by-product, the classical Demkov–Fradkin tensor for the classical curved harmonic oscillator has been obtained by the same method. The case of two dimensions has been worked out in detail: Here, the operators close a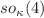 
Lie algebra; the spectrum and eigenfunctions are explicitly solved in an algebraic way and in the classical case the trajectories have been computed.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
