https://doi.org/10.1140/epjp/s13360-025-05993-y
Regular Article
Multi-dimensional q-Gaussian densities describing systems of confined interacting particles with drag
1
Departamento de Física, Universidad Católica del Norte, Av. Angamos 0610, 1270709, Antofagasta, Chile
2
CeBio y Departamento de Ciencias Básicas, Universidad Nacional del Noroeste de la Província de Buenos Aires, UNNOBA-Conicet, Roque Saenz Peña 456, Junin, Argentina
3
Centro Brasileiro de Pesquisas Físicas and National Institute of Science and Technology for Complex Systems, Rua Xavier Sigaud 150, 22290-180, Rio de Janeiro, RJ, Brazil
Received:
4
November
2024
Accepted:
7
January
2025
Published online:
15
January
2025
Fokker–Planck equations with power-law nonlinearities in the diffusion term are useful for the description of various complex systems in physics and other disciplines. These evolution equations provide an effective representation of overdamped systems of particles interacting through short-range forces and confined by an external potential. It has been recently shown that the nonlinear Fokker–Planck equation admits an embedding within a Vlasov-like mean-field equation that allows to incorporate inertial effects to the associated dynamics. Exact time-dependent solutions of the q-Gaussian form (with compact support) of the Vlasov-like equation have been found for one-dimensional systems with quadratic confining potentials. In the present contribution, we explore the possibility of extending this type of solutions to multi-dimensional systems with N spatial dimensions. We found exact time-dependent q-Gaussian solutions in 
and 
, and investigate their main properties. We also prove that this type of solutions does not exist in systems with spatial dimension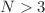 
.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
