https://doi.org/10.1140/epjp/s13360-024-05898-2
Regular Article
Dynamics of a stochastic tumor–immune interaction system
School of Physical and Mathematical Sciences, Nanjing Tech University, 211816, Nanjing, Jiangsu, China
Received:
7
October
2024
Accepted:
30
November
2024
Published online:
10
December
2024
To investigate the effects of environmental factors on tumor growth and the immune response, we have developed a stochastic model of the tumor–immune system, which encompasses tumor cells, NK cells, CD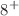
T cells, and dendritic cells. Initially, we analyzed the deterministic version of the system, deriving the threshold conditions for the local asymptotic stability of the equilibrium point in accordance with the stability theory of differential equations. For the stochastic version, we utilized Itô’s formula and Lyapunov analysis techniques to confirm the existence of a unique global positive solution and to identify sufficient conditions for the mean persistence of the system. Furthermore, we applied the stochastic maximum principle to devise optimal control strategies for the prevention and control of tumor cell proliferation. Our numerical simulations reveal that varying levels of noise intensity result in different outcomes for tumor cells, NK cells, CD 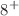T cells, and dendritic cells, including persistence and extinction. These findings offer critical insights that can guide the development of strategies for preventing and managing tumor progression.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
