https://doi.org/10.1140/epjp/s13360-024-05848-y
Regular Article
Numerical and analytical study of Rayleigh–Bénard convection with Kuvshiniski fluid in an inclined plane
1
Department of Mathematics, Bharathiar University, 641 046, Coimbatore, Tamil Nadu, India
2
Department of Mathematics, Faculty of Sciences AlZufi, Majmaah University, 11952, Majmaah, Saudi Arabia
Received:
11
September
2024
Accepted:
15
November
2024
Published online:
8
December
2024
This study investigates double diffusive convection in a viscoelastic Kuvshiniski fluid within a horizontal channel, focusing on the impact of various parameters on thermal stability and flow behaviour. Utilising the Lorenz amplitude model and the Runge–Kutta–Fehlberg (RKF45) technique, we analyse the governing equations under specific conditions. The parametric values considered include Rayleigh numbers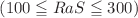
, Prandtl numbers 
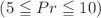, and Lewis numbers 
. Our results indicate that increasing the Lewis number enhances thermal stability, delaying the onset of convection. Additionally, the Nusselt number (Nu) exhibits a significant increase with higher Rayleigh numbers, with values reaching up to 25.5 for RaS = 300, indicating improved heat transfer efficiency. The study also reveals that the Kuvshiniski fluid parameter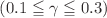 
plays a crucial role in modulating flow characteristics, with nonlinear stability results demonstrating a transition from stable to unstable regimes as 
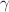increases. These findings contribute to a deeper understanding of double diffusive convection in non-Newtonian fluids and have implications for various industrial and geophysical applications.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
