https://doi.org/10.1140/epjp/s13360-024-05806-8
Regular Article
Lie symmetries and invariant solutions for three generalized short pulse equations
1
Department of Mathematics, University of Punjab, Lahore, Pakistan
2
Division of Science and Technology, Department of Mathematics, University of the Education, Lahore, Pakistan
Received:
19
August
2024
Accepted:
5
November
2024
Published online:
18
November
2024
The basic idea of Lie symmetry analysis, LSA, is to find the similarity solutions, invariant solutions and the reduction of order of non-linear PDEs that are formed under a local one-parameter Lie group of transformations of dependent and independent variables. Sophus Lie was a Norwegian mathematician whose work played fundamental role for attaining the solutions of non-linear PDEs and their systems by following a certain algorithm which is comparatively more easy than other complex methods. In this article, LSA is applied for further three different new cases of non-linear short pulse equation (SPE). We in fact obtain invariant solutions and reductions under the one-parameter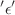 
Lie group of transformations. Then we derive traveling wave solutions for the first case of SPE by sine-cosine method.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
