https://doi.org/10.1140/epjp/s13360-024-05803-x
Regular Article
Multiple quantum harmonic oscillators in the Tsallis statistics
Department of Economics, Faculty of Economics, Chiba Keizai University, 263-0021, Chiba, Japan
a
masamichi.ishihara.research@gmail.com
Received:
7
June
2024
Accepted:
5
November
2024
Published online:
19
November
2024
We studied multiple quantum harmonic oscillators in the Tsallis statistics of entropic parameter q in the cases that the distributions are power-like, separately applying the conventional expectation value, the unnormalized q-expectation value, and the normalized q-expectation value (escort average). We obtained the expressions of the energy and the Tsallis entropy, using the Barnes zeta function. For the same oscillators, we obtained the expressions of the energy, the Tsallis entropy, the average level of the oscillators, and the heat capacity. Numerically, we calculated the energy, the Tsallis entropy, and the heat capacity for various N and q, using the expansion of the Barnes zeta function with the Hurwitz zeta function, where N is the number of independent oscillators. The parameter q is less than one in the Tsallis statistics with the conventional expectation value. The parameter q is greater than one in both sets of the Tsallis statistics, each of which is defined with a different q-expectation value. These limitations of q arise from the requirements that the distributions are power-like. It was shown from the requirements for the Barnes zeta function that q is greater than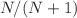 
for the conventional expectation value and that q is less than 
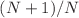for both of the q-expectation values. In the Tsallis statistics with the conventional expectation value, the energy, the Tsallis entropy, and the heat capacity decrease with q. These quantities per oscillator increase with N. In the Tsallis statistics with the unnormalized q-expectation value, the energy, the Tsallis entropy, and the heat capacity increase with q at low temperature, while decrease with q at high temperature. These quantities per oscillator increase with N at low temperature, while decrease with N at high temperature. The heat capacity is the Schottky-type. The quantities are affected by the zero-point energy. In the Tsallis statistics with the normalized q-expectation value, the N dependence of the energy per oscillator and that of the heat capacity per oscillator are quite weak, and the q dependence of the energy and that of the heat capacity are also weak, when the equilibrium temperature, which is often called the physical temperature, is adopted. The Tsallis entropy per oscillator decreases with N and the Tsallis entropy decreases with q.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
