https://doi.org/10.1140/epjp/s13360-024-05796-7
Regular Article
Landau and leading singularities in arbitrary space-time dimensions
1
Dipartimento di Fisica e Astronomia, Università degli Studi di Padova, Via Marzolo 8, 35131, Padova, Italy
2
INFN, Sezione di Padova, Via Marzolo 8, 35131, Padova, Italy
3
Max-Planck-Institut für Physik, Werner-Heisenberg-Institut, Föhringer Ring 6, 80805, München, Germany
4
Department of Mathematical Sciences, University of Liverpool, L69 3BX, Liverpool, UK
Received:
24
April
2024
Accepted:
31
October
2024
Published online:
24
November
2024
Using the decomposition of the D-dimensional space-time into parallel and perpendicular subspaces, we study and prove a connection between Landau and leading singularities for N-point one-loop Feynman integrals by applying the multidimensional theory of residues. We show that if 
and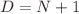 
, the leading singularity corresponds to the inverse of the square root of the leading Landau singularity of the first and second type, respectively. We make use of this outcome to systematically provide differential equations of Feynman integrals in canonical forms and the extension of the connection of these singularities at the multi-loop level by exploiting the loop-by-loop approach. Illustrative examples with the calculation of Landau and leading singularities are provided to supplement our results.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
