https://doi.org/10.1140/epjp/s13360-024-05329-2
Regular Article
General proof of the Tolman law
Department of Physics, Beijing Normal University, 100875, Beijing, China
Received:
24
February
2024
Accepted:
26
May
2024
Published online:
8
June
2024
Tolman proposed that the proper temperature T of a static self-gravitating fluid in thermodynamic equilibrium satisfies the relation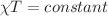 
, where 
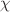is the redshift factor of the spacetime. The Tolman law has been proven for radiation in stationary spacetimes and for perfect fluids in stationary, asymototically flat and axisymmetric spacetimes. It is unclear whether the proof can be extended to more general cases. In this paper, we prove that under some reasonable conditions, the Tolman law always holds for a perfect fluid in a stationary spacetime. The key assumption in our proof is that the particle number density n can not be determined by energy density 
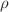and pressure p via the equations of state. This is true for most known fluids with the equation of state 
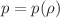. Then, by requiring that the total entropy of the fluid is an extremum for the variation of n with a fixed metric and stress-energy tensor, we prove the Tolman law. In our proof, only local conservation laws are used and no global conditions are imposed on the spacetime. Our work suggests that the Tolman law holds for a generic perfect fluid in a stationary spacetime, even beyond general relativity.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
