https://doi.org/10.1140/epjp/s13360-024-05307-8
Regular Article
On the completeness of the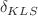 
-generalized statistical field theory
Departamento de Física, Universidade Federal do Piauí, 64049-550, Teresina, PI, Brazil
Received:
25
April
2024
Accepted:
23
May
2024
Published online:
5
June
2024
In this work, we introduce a field-theoretic tool that enable us to evaluate the critical exponents of 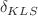-generalized systems undergoing continuous phase transitions, namely 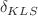-generalized statistical field theory. It generalizes the standard Boltzmann–Gibbs through the introduction of the 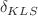parameter from which Boltzmann–Gibbs statistics is recovered in the limit 
. From the results for the critical exponents, we provide the referred physical interpretation for the 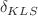parameter. Although new generalized universality classes emerge, we show that they are incomplete for describing the behavior of some real materials. This task is fulfilled only for nonextensive statistical field theory, which is related to fractal derivative and multifractal geometries, up to the moment, for our knowledge.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
