https://doi.org/10.1140/epjp/s13360-023-04816-2
Regular Article
The circular Sisyphus random walk model
1
The Ruppin Academic Center, 40250, Emeq Hefer, Israel
2
The Hadassah Academic College, 91010, Jerusalem, Israel
Received:
1
November
2023
Accepted:
20
December
2023
Published online:
9
January
2024
We study, using analytical techniques, the time-dependent behavior of the circular Sisyphus random walk model, an infinite stochastic Markov chain whose dynamics is determined by the following jumping rule: at every discrete time step the walker has a finite probability q to move one step upward toward her target at the top of the ‘ladder’ and a complementary probability 
to fall back to her initial position, resulting in the need to restart the climbing process. A climber who reaches her target after making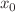 
upward steps in a row (without a single stumble in between) is doomed to restart the circular Sisyphean process all over again from the bottom of the ladder. We determine the time-dependent success rate function 
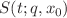of the system, the fraction of circular Sisyphus random climbers who reach their target after making exactly t steps. We identify a special family of initial conditions that leads to stationary configurations of the circular random climbers with constant (time-independent) success rate functions. Interestingly, it is explicitly proved that, for generic initial conditions, the characteristic relaxation time of the system toward an equilibrium steady-state configuration is independent of the size 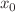of the system and it diverges in the deterministic 
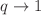limit. The analytically derived results are used to analyze the underlying dynamics of the ‘conditional success game’, a highly risky investment strategy in which a reward 
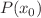, which is a monotonically increasing function of the height 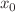of the challenge, is offered to agents who succeed in making 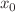successful steps in a row.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
