https://doi.org/10.1140/epjp/s13360-023-04631-9
Regular Article
A robust study of dual variants of SARS-CoV-2 using a reaction-diffusion mathematical model with real data from the USA
Department of Mathematics, Faculty of Science, King Mongkut’s University of Technology Thonburi (KMUTT), 126 Pracha Uthit Rd., Bang Mod, Thung Khru, 10140, Bangkok, Thailand
Received:
19
September
2023
Accepted:
25
October
2023
Published online:
29
November
2023
This study proposes a mathematical model to analyze the transmission mechanism of SARS-CoV-2 using a reaction-diffusion framework. The importance of incorporating diffusion in mathematical models of SARS-CoV-2 is emphasized, as it can lead to a more accurate understanding of disease spread and inform effective public health interventions. The impact of diffusion effects on the SARS-CoV-2 epidemic model has been significant, as the virus has rapidly spread across the globe since it was first identified in late 2019. The speed and efficiency of transmission have been a key factor in the severity of the pandemic, as many individuals may be asymptomatic or experience mild symptoms, making it difficult to identify and control the spread of the virus. The model includes six classes, namely Susceptible, Exposed to strain 1 SARS-CoV-2 and strain 2 SARS-CoV-2, infected by strain 1 SARS-CoV-2 and strain 2 SARS-CoV-2, and Recovered or Removed (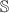
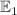
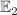
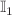
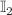
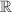), which are dependent on both time and space. This study uses the next-generation matrix approach to calculate the threshold number 
and estimates parameter values through the use of least squares curve fitting tools. A combination of the operator splitting approach, finite difference method, and Crank–Nicolson method is used to simulate the model. The study looks at how stable the disease-free and endemic equilibrium points are, and it performs sensitivity analysis to look at the effects of different parameters. The simulation results of the model are compared in detail with and without diffusion and are verified through mutual comparison and theoretical analysis to ensure the accuracy of the solution. This study provides valuable insights into the transmission mechanism of SARS-CoV-2 and has important implications for public health policy.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
