https://doi.org/10.1140/epjp/s13360-023-04578-x
Regular Article
Bursting oscillation and mechanism analysis of a class of Duffing–Van der Pol system with two excitation terms
School of Mathematical Sciences, Zhejiang Normal University, 321004, Jinhua, China
Received:
10
August
2023
Accepted:
9
October
2023
Published online:
15
November
2023
Bursting oscillation is a common dynamical behavior observed in the systems with multi-time scales that finds significant practical applications. This study focuses on a class of fast–slow coupled Duffing–van der Pol system with two periodic excitation terms. The equilibrium and the bifurcation stability are analyzed, and the stability and bifurcation direction of the Hopf bifurcation are evaluated. We simplify the two excitations using the De Moivre formula, transforming them into an excitation function. Therefore, we can study the bursting oscillation using the fast–slow dynamic analysis method. We discovered that bursting occurs at different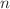 
when the parameters take different values. Meanwhile, we talk about the delayed bifurcation phenomenon of the subHopf bifurcation point and how the amplitudes affect bursting.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
