https://doi.org/10.1140/epjp/s13360-023-04470-8
Regular Article
Solitary waves solutions and local conserved vectors for extended quantum Zakharov–Kuznetsov equation
1
Department of Mathematics, Faculty of Science, University of Botswana, Private Bag 22, Gaborone, Botswana
2
Department of Mathematical Sciences, North-West University, Private Bag X2046, Mafikeng Campus, 2735, Mmabatho, Republic of South Africa
3
Department of Mathematical Sciences, University of South Africa, UNISA, 0003, Pretoria, Republic of South Africa
Received:
10
June
2023
Accepted:
11
September
2023
Published online:
30
September
2023
This paper studies a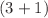 
-dimensions extended quantum Zakharov–Kuznetsov (qZK) equation. The quantum Zakharov–Kuznetsov (qZK) equation models several physical phenomena such as ion-acoustic waves in a magnetized plasma composed of cold ions and hot isothermal electrons. The quantum plasmas and their new structures have attracted researchers at both experimental and theoretical level. The powerfulness of this equation resulted in many scholars finding closed-form solutions of this equation so as to have exhaustive understanding of certain physical features embedded in the qZK equation. Soliton solutions have become one of the most significant solutions in solving nonlinear evolution equations (NLEEs) due to their applications in different physical fields like plasma physics, solid state physics, neural physics and diffusion process. With this reason, we aim to implement ansatz methods to derive a variety of soliton solutions such as bright, singular and dark solitary waves solutions. Furthermore, we will construct local conservation laws via the variational approach. Thereafter, the dynamical behaviors through graphical representation of the derived solutions will be discussed in detail.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
