https://doi.org/10.1140/epjp/s13360-023-04270-0
Regular Article
Multi-soliton solutions for the two-component modified short pulse equation and its nonlocal reductions via Bäcklund transformations
School of Mathematics and Statistics, Nanning Normal University, 530001, Nanning, Guangxi, People’s Republic of China
Received:
21
February
2023
Accepted:
8
July
2023
Published online:
29
August
2023
Using the reciprocal transformation and the associated equation, a Bäcklund transformation (BT) involving both independent and dependent variables is constructed and studied for the two-component modified short pulse (2mSP) equation. Through the permutability property, the related nonlinear superposition formula (NSF) and multi-BT are worked out. The multi-soliton solutions of the 2mSP equation are also constructed by means of multi-BT. By reducing the soliton solutions of the 2mSP equation, multi-soliton solutions for the four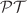 
symmetric nonlocal reductions, which are the real (complex) reverse space-time nonlocal focusing (defocusing) mSP equations, are calculated respectively. In particular, the multi-cuspon-like solutions and multi-breather-like solutions with the influence of nonlocality as well as their interaction are presented.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
