https://doi.org/10.1140/epjp/s13360-023-04286-6
Regular Article
Dynamics and simulation of stochastic COVID-19 model using higher-order numerical scheme
1
Department of Mathematics, City University of Science and Information Technology Peshawar, Peshawar, Pakistan
2
Department of Mathematics, Facility of Applied Science, King Mongkut’s University of Technology North Bangkok, Bangkok, Thailand
3
Department of Mathematics, Faculty of Science, University of Tabuk, P.O.Box 741, 71491, Tabuk, Saudi Arabia
Received:
27
April
2023
Accepted:
16
July
2023
Published online:
31
July
2023
This article describes how mathematical models can be used to depict the number of people who have been tested for the deadly coronavirus that is currently sweeping the globe. It also includes information about the number of people who have been diagnosed with the virus, as well as the number of people who have recovered from it. It is unknown whether or if long-term immunity is imparted by beating a COVID-19 infection, and if so, for how long. We hope this study will help us forecast the outbreak more precisely in future. We create a mathematical model that describes the dynamics of a COVID-19 infection by including a class of isolation. The model’s formulation is discussed first, followed by its advantages. The suggested model’s (global and local) stability is proven, and it is shown to be dependent on the basic reproduction. In order to numerically solve the suggested model, the Legendre spectral method is used, where the convergence orders of the proposed method is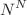 
, which is higher than finite difference and finite element methods. Moreover, a visual representation of the findings is presented. Our findings provide more evidence that interpersonal interaction among humans contributes to the dissemination of COVID-19 pandemic. As a result, isolating the affected individual may reduce the spread of COVID-19 in the future.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
