https://doi.org/10.1140/epjp/s13360-023-04254-0
Regular Article
Relation between the escort average in microcanonical ensemble and the escort average in canonical ensemble in the Tsallis statistics
Department of Food and Nutrition, Koriyama Women’s University, 963-8503, Koriyama, Fukushima, Japan
Received:
26
May
2023
Accepted:
5
July
2023
Published online:
15
July
2023
We studied the escort averages in microcanonical and canonical ensembles in the Tsallis statistics of entropic parameter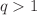 
. The quantity 
is the measure of the deviation from the Boltzmann–Gibbs statistics. We derived the relation between the escort average in the microcanonical ensemble and the escort average in the canonical ensemble. Conditions arise by requiring that the integrals appeared in the canonical ensemble do not diverge. A condition is the relation between the heat capacity 
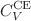at constant volume in the canonical ensemble and the entropic parameter q: 
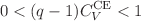. This condition gives the known condition when 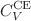equals the number of ingredients N. With the derived relation, we calculated the energy, the energy fluctuation, and the difference between the canonical ensemble and the microcanonical ensemble in the expectation value of the square of Hamiltonian. The difference between the microcanonical ensemble and the canonical ensemble in energy is small because of the condition. The heat capacity 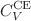and the quantity are related to the energy fluctuation and the difference. It was shown that the magnitude of the relative difference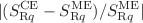 
is small when the number of free particles is large, where 
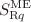is the Rényi entropy in the microcanonical ensemble and 
is the Rényi entropy in the canonical ensemble. The similar result was also obtained for the Tsallis entropy.
Copyright comment corrected publication 2023
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. corrected publication 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
