Geometrical and physical interpretation of the Levi-Civita spacetime in terms of the Komar mass density

Bence Racskó; László Á. Gergely

doi:10.1140/epjp/s13360-023-04027-9

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Open Access

Eur. Phys. J. Plus (2023) 138: 413
https://doi.org/10.1140/epjp/s13360-023-04027-9

Regular Article

Geometrical and physical interpretation of the Levi-Civita spacetime in terms of the Komar mass density

Bence Racskó¹^,2^a and László Á. Gergely¹^,2^b

¹ Institute of Physics, University of Szeged, Tisza Lajos krt., 6720, Szeged, Hungary
² Department of Theoretical Physics, Wigner Research Centre for Physics, Konkoly-Thege Miklós u. 29-33, 1121, Budapest, Hungary

^a racsko@titan.physx.u-szeged.hu
^b laszlo.arpad.gergely@gmail.com

Received: 9 December 2022
Accepted: 24 April 2023
Published online: 16 May 2023

Abstract

We revisit the interpretation of the cylindrically symmetric, static vacuum Levi-Civita metric, known in either Weyl, Einstein–Rosen, or Kasner-like coordinates. The Komar mass density of the infinite axis source arises through a suitable compactification procedure. The Komar mass density $μ_{K}$ $\mu _{K}$ calculated in Einstein–Rosen coordinates, when employed as the metric parameter, leads to a number of advantages. It eliminates double coverages of the parameter space, vanishes in flat spacetime and when small, it corresponds to the mass density of an infinite string. After a comprehensive analysis of the local and global geometry, we proceed with the physical interpretation of the Levi-Civita spacetime. First we show that the Newtonian gravitational force is attractive and its magnitude increases monotonically with all positive $μ_{K}$ $\mu _{K}$ , asymptoting to the inverse of the proper distance in the radial direction. Second, we reveal that the tidal force between nearby geodesics (hence gravity in the Einsteinian sense) attains a maximum at $μ_{K} = 1 / 2$ $\mu _{K}=1/2$ and then decreases asymptotically to zero. Hence, from a physical point of view the Komar mass density of the Levi-Civita spacetime encompasses two contributions: Newtonian gravity and acceleration effects. An increase in $μ_{K}$ $\mu _{K}$ strengthens Newtonian gravity but also drags the field lines increasingly parallel, eventually transforming Newtonian gravity through the equivalence principle into a pure acceleration field and the Levi-Civita spacetime into a flat Rindler-like spacetime. 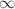In a geometric picture the increase of $μ_{K}$ $\mu _{K}$ from zero to $\infty$ $\infty$ deforms the planar sections of the spacetime into ever deepening funnels, eventually degenerating into cylindrical topology in an appropriately chosen embedding.

Bence Racskó and László Á. Gergely have contributed equally to this work.

Supplementary Information The online version contains supplementary material available at https://doi.org/10.1140/epjp/s13360-023-04027-9.

© The Author(s) 2023

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.