https://doi.org/10.1140/epjp/s13360-023-03925-2
Regular Article
Mean and Gaussian curvatures of equilibrium states for a spin-1 Ising system: existence of minimal surface in the paramagnetic solutions
Department of Physics, Akdeniz University, 07058, Antalya, Türkiye
a rerdem@akdeniz.edu.tr, rizaerdem07@gmail.com
Received:
16
January
2023
Accepted:
21
March
2023
Published online:
1
April
2023
We present an approach to analyze the equilibrium states in a spin-1 Ising model with bilinear and biquadratic interactions using mean (H) and Gaussian (K) curvatures of the mean-field free energy surface. From the temperature variation of H and K, we have reported the local shapes of equilibrium free energies for the paramagnetic, ferromagnetic and quadrupolar solutions. It is important to mention that a minimal surface for the paramagnetic case with 
, 
is explicitly observed. For the ferromagnetic case, it is found that the curvature H displays a cusp singularity at the criticality with the exponent values of 
and a convergence of K is observed with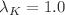 
.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
