https://doi.org/10.1140/epjp/s13360-023-03656-4
Regular Article
Application of Ramsey theory to localization of set of product states via multicopies
School of Mathematics, South China University of Technology, 510641, Guangzhou, China
Received:
30
August
2022
Accepted:
3
January
2023
Published online:
20
January
2023
It is well known that any N orthogonal pure states can always be perfectly distinguished under local operation and classical communications (LOCC) if 
copies of the state are available (Walgate et al. Phys. Rev. Lett. 85, 4972 (2000)). It is important to reduce the number of quantum state copies that ensures the LOCC distinguishability in terms of resource saving and nonlocality strength characterization. Denote 
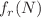the least number of copies needed to LOCC distinguish any N orthogonal r-partite product states. This work will be devoted to the estimation of the upper bound of 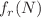. In fact, we first relate this problem with Ramsey theory, a branch of combinatorics dedicated to studying the conditions under which orders must appear. Subsequently, we prove 
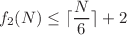, which is better than 
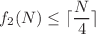obtained in Shu (Eur. Phys. J. Plus 136, 1172 (2021)) when 
. We further exhibit that for arbitrary 
, 
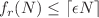always holds for sufficiently large N.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2023. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
