https://doi.org/10.1140/epjp/s13360-022-03029-3
Regular Article
Sextic anharmonic oscillators and Heun differential equations
1
Instituto de Matemática, Universidad Autónoma de Santo Domingo, Santo Domingo, Dominican Republic
2
Department of Mathematics, University of Central Florida, 32816, Orlando, Florida, USA
3
School of Mathematical and Computational Sciences, University of Prince Edward Island, 550 University Avenue, C1A 4P3, Charlottetown, PEI, Canada
Received:
17
May
2022
Accepted:
1
July
2022
Published online:
20
July
2022
With certain constraints on the parameters 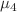 and
and 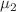 , it is known that the Schrödinger equation with the sextic anharmonic oscillator potential
, it is known that the Schrödinger equation with the sextic anharmonic oscillator potential 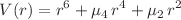 is quasi-exactly solvable. Here, we solve the Schrödinger equation for arbitrary values of the potential parameters in the d-dimensional case. The method discussed offers a practical solution to the biconfluent Heun equation’s eigenvalue problem. A technique based on the asymptotic iteration method is used to evaluate the coefficients of the series solutions for arbitrary
is quasi-exactly solvable. Here, we solve the Schrödinger equation for arbitrary values of the potential parameters in the d-dimensional case. The method discussed offers a practical solution to the biconfluent Heun equation’s eigenvalue problem. A technique based on the asymptotic iteration method is used to evaluate the coefficients of the series solutions for arbitrary 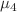 and
and 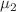 .
.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2022




