Analytic simulation of MHD boundary layer flow of a chemically reacting upper-convected Maxwell fluid past a vertical surface subjected to double stratifications with variable properties

Md. Fayz-Al-Asad; Tosin Oreyeni; Mehmet Yavuz; Philip O. Olanrewaju

doi:10.1140/epjp/s13360-022-03014-w

2024 Impact factor 2.9

EPJ PLUS - Condensed Matter and Complex Systems

Eur. Phys. J. Plus (2022) 137: 813
https://doi.org/10.1140/epjp/s13360-022-03014-w

Regular Article

Analytic simulation of MHD boundary layer flow of a chemically reacting upper-convected Maxwell fluid past a vertical surface subjected to double stratifications with variable properties

Md. Fayz-Al-Asad¹^a, Tosin Oreyeni², Mehmet Yavuz³^c and Philip O. Olanrewaju⁴

¹ Department of Mathematics, Bangladesh University of Engineering and Technology, 1000, Dhaka, Bangladesh
² Department of Physical Sciences, Precious Cornerstone University, Ibadan, Nigeria
³ Department of Mathematics and Computer Sciences, Faculty of Science, Necmettin Erbakan University, 42090, Konya, Türkiye
⁴ Department of Mathematics and Statistics, Federal University Wukari, Wukari, Nigeria

^a fayzmath.buet@gmail.com
^c mehmetyavuz@erbakan.edu.tr

Received: 3 December 2021
Accepted: 27 June 2022
Published online: 14 July 2022

Abstract

The study of thermal stratification has a broad scope of applications in solar engineering owing to its ability to predict the cases of achieving superior energy efficiency. This present communication focuses on the flow of a free convective MHD upper-convected Maxwell fluid in concert temperature-dependent viscosity, thermal conductivity across a stratified surface with nth order of chemical reaction. The governing partial differential equations are transformed into nonlinear ordinary differential equations by introducing relevant similarity variables and approximate analytical solution is determined operating the homotopy analysis method. Influence of different relevant parameters such as Deborah number, stratification, chemical reaction and variable thermophysical parameters on temperature, velocity and concentration distributions is shown to highlight the specifics of heat and mass transfer flow characteristics. 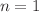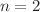It is followed that for the cases of $n = 1$ $$n=1$$ and $n = 2$ $$n=2$$ , the concentration of species reduces for increasing chemical reaction parameter. It is also noticed that, the values of 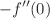$- f^{''} (0)$ $$-f''(0)$$ decrease while $- θ^{'} (0)$ $-\theta '(0)$ and $- ϕ (0)$ $-\phi (0)$ increase with increasing Deborah number $β$ $\beta$ .