Eur. Phys. J. Plus (2022) 137: 674
https://doi.org/10.1140/epjp/s13360-022-02897-z

Regular Article

Dispersive solitary wave solutions for the dynamical soliton model by three versatile analytical mathematical methods

Department of Mathematics, Faculty of Science, University of Gujrat, 50700, Gujrat, Pakistan

^c jamshadahmadm@gmail.com

Received: 24 July 2021
Accepted: 28 May 2022
Published online: 8 June 2022

Abstract

The solitary wave solutions gained well-reputed significance because of their peculiar characteristics. Solitary waves are spatially localized waves and are found in a variety of natural systems from mathematical physics and engineering phenomena. This manuscript deals the different solitary wave solutions that have a great significance in mathematical physics. Various solutions are recovered in single and combo shapes like bright, dark, singular, bright-dark, and dark-singular solitons by the virtue of the generalized exponential rational function method (GERFM), (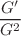)-expansion function method and the generalized Kudryashov method. Besides, the singular periodic wave and rational function solutions are also derived. The physical behavior of the reported results is sketched through several 3 dimensional, and 2 dimensional profiles with the assistance of suitable parameters. The acquired results are valuable in grasping the elementary scenarios of nonlinear sciences as well as in the related nonlinear higher dimensional wave fields. The achieved outcomes have been verified by putting them into the governing equation with the aid of Mathematica. Thus our strategies through the fortress of representative calculations give a functioning and intense mathematical execute for tackling complicated nonlinear wave problems. We anticipate, it will contribute us to observe the waves that occur in nonlinear complicated phenomenas. We believe that this work is timely and will be of interest to a broad range of experts involved in modeling.