Eur. Phys. J. Plus (2022) 137: 659
https://doi.org/10.1140/epjp/s13360-022-02863-9

Regular Article

On a moment analysis of the stochastic nuclear reactor dynamics

Engineering Department, Shahid Beheshti University, P. O. Box. 1983969411, Tehran, Iran

^a mo_zarei@sbu.ac.ir

Received: 10 March 2022
Accepted: 23 May 2022
Published online: 4 June 2022

Abstract

The kinetic behavior of neutron population at a low power operating reactor is essentially governed by a set of stochastic differential equations. In this work, interesting features of an Ito representation for the point kinetics equations are investigated through first and second order moment analysis of the pertaining Fokker–Planck equation. A parametric stability analysis by way of the local Jacobians obtained at the initial quiescent operating point was carried out for these models subject to a step reactivity insertion. A change in the sign of the corresponding eigenvalues were inspected at the threshold value of ${\rho }_{\text{ext}}=\left|{\rho }_{\text{sub}}\right|$. The consequent transients are however stabilized thereafter at an attractor equilibrium point. While these temporal profiles are coincident at ${\rho }_{\text{ext}}<\left|{\rho }_{\text{sub}}\right|$ for all the Ito, first and second moments, noticeable discrepancy is observed between the second moment profile and those of the first moment and the original Ito model at 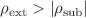${\rho }_{\text{ext}}>\left|{\rho }_{\text{sub}}\right|$. The latter case alludes to large deviations from the mean neutron population encountered throughout the “super-critical” neutron population build-up regime. This outcome may be a consequence of the small fluctuation validity of the Fokker Planck formalism as a second order Taylor approximation to the original master equation. The pertaining probability distribution is thus appropriately reflected through the second moment only if higher order terms are incorporated in the underlying Taylor expansion.