Eur. Phys. J. Plus (2022) 137: 366
https://doi.org/10.1140/epjp/s13360-022-02542-9

Regular Article

Global dynamics and evolution for the Szekeres system with nonzero cosmological constant term

¹ Departamento de Matemáticas, Universidad Católica del Norte, Avda. Angamos 0610, Casilla 1280, Antofagasta, Chile
² Institute of Systems Science, Durban University of Technology, PO Box 1334, 4000, Durban, South Africa
³ Instituto de Ciencias Físicas y Matemáticas, Universidad Austral de Chile, 5090000, Valdivia, Chile

^b genly.leon@ucn.cl

Received: 11 January 2022
Accepted: 28 February 2022
Published online: 19 March 2022

Abstract

The Szekeres system with cosmological constant term describes the evolution of the kinematic quantities for Einstein field equations in 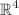${\mathbb{R}}^4$. In this study, we investigate the behavior of trajectories in the presence of cosmological constant. It has been shown that the Szekeres system is a Hamiltonian dynamical system. It admits at least two conservation laws, h and 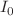$I_0$ which indicate the integrability of the Hamiltonian system. We solve the Hamilton–Jacobi equation, and we reduce the Szekeres system from 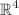${\mathbb{R}}^4$ to an equivalent system defined in 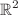${\mathbb{R}}^2$. Global dynamics are studied where we find that there exists an attractor in the finite regime only for positive valued cosmological constant and $I_0<-2.08$. Otherwise, trajectories reach infinity. 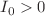For $I_0>0$ the origin of trajectories in 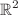${\mathbb{R}}^2$ is also at infinity. Finally, we investigate the evolution of physical properties by using dimensionless variables different from that of Hubble-normalization conducing to a dynamical system in 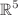${\mathbb{R}}^5$. We see that the attractor at the finite regime in 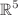${\mathbb{R}}^5$ is related with the de Sitter universe for a positive cosmological constant.