https://doi.org/10.1140/epjp/s13360-022-02472-6
Regular Article
Incommensurate Fractional Discrete Neural Network: chaos and complexity
1
Department of Mathematics, The University of Jordan, 11942, Amman, Jordan
2
Department of Mathematics and Computer Science, University of Larbi Ben M’hidi, Oum El Bouaghi, Algeria
Received:
21
January
2022
Accepted:
10
February
2022
Published online:
17
February
2022
In this research, we offer a novel discrete-time fractional Hopfield neural network (DTHNN) with incommensurate order. Analytical and numerical analysis by employing maximum Lyapunov exponents, phase attractors, bifurcation diagrams, and the 0-1 test is used to investigate the dynamical behavior of the proposed neural network. In particular, the stability of the zero equilibrium point is studied in order to show that the DTHNN with incommensurate fractional order converges to zero point. Moreover, in order to establish the presence of chaos, an analysis of complexity is performed utilizing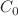 
complexity and approximate entropy (ApEn). Finally, simulations on MATLAB will be performed to test the validity of the results presented.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2022
