https://doi.org/10.1140/epjp/s13360-021-01903-0
Regular Article
Regularization of central forces with damping in two and three dimensions
1
School of Physics, University of Hyderabad, Central University P.O, 500046, Hyderabad, Telangana, India
2
Department of Mathematics, Khalifa University of Science and Technology, P.O. Box 127788, Abu Dhabi, UAE
Received:
23
June
2021
Accepted:
26
August
2021
Published online:
3
September
2021
Regularization of damped motion under central forces in two and three dimensions is investigated and equivalent; undamped systems are obtained. The dynamics of a particle moving in 
potential and subjected to a damping force is shown to be regularized using Levi-Civita transformation. We then generalize this regularization mapping to the case of damped motion in the potential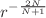 
. Further equation of motion of a damped Kepler motion in three dimensions is mapped to an oscillator with inverted sextic potential and couplings, in four dimensions using Kustaanheimo–Stiefel regularization method. It is shown that the strength of the sextic potential is given by the damping coefficient of the Kepler motion. Using homogeneous Hamiltonian formalism, we establish the mapping between the Hamiltonian of these two models. Both in two and three dimensions, we show that the regularized equation is nonlinear, in contrast to undamped cases. Mapping of a particle moving in a harmonic potential subjected to damping to an undamped system with shifted frequency is then derived using Bohlin–Sundman transformation.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2021
