https://doi.org/10.1140/epjp/s13360-021-01865-3
Regular Article
Asymptotic controllability of nonlinear Fokker–Planck equations
Al.I. Cuza University, and Octav Mayer Institute of Mathematics of the Romanian Academy, Iaşi, Romania
Received:
18
January
2021
Accepted:
10
August
2021
Published online:
1
September
2021
We discuss here the asymptotic controllability problem for the Fokker–Planck equations,
ρt − Δβ(ρ) + div(uρ) = 0 in (0, ∞) × ℝd,
ρ(0, x) = ρ0(x), x ∈ ℝd,
that is, the existence of a feedback controller 
such that 
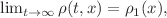a.e.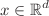 
, where 
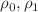are given probability densities and 
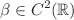is a monotonically increasing function. In this work, it is designed such a controller u for a certain class of final states 
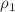which is identified. This problem is related to the controllability of McKean-Vlasov stochastic differential equations and the approach used here relies on the H-theorem established in (Barbu, Rockner in Indiana Univ Math J, 2020), Theorem 6.1, for nonlinear and nondegenerate Fokker–Planck equations.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2021
