https://doi.org/10.1140/epjp/s13360-021-01864-4
Regular Article
Hölder continuity of mild solutions of space-time fractional stochastic heat equation driven by colored noise
1
Faculty of Mathematics and Applications, Sai Gon University, Ho Chi Minh City, Viet Nam
2
Department of Mathematics and Computer Science, University of Science-VNUHCM, 227 Nguyen Van Cu Str., Dist. 5, Ho Chi Minh City, Viet Nam
3
Department of Mathematics, Faculty of Science, Nong Lam University, Ho Chi Minh City, Viet Nam
b
nhtuan@hcmus.edu.vn
c
tranbaongoc@hcmuaf.edu.vn
Received:
14
May
2021
Accepted:
10
August
2021
Published online:
13
September
2021
An initial value problem for space-time fractional stochastic heat equations driven by colored noise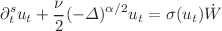 
has been discussed in this work. Here, 
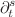and 
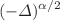stand for the Caputo’s fractional derivative of order 
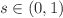and the fractional Laplace operator of order 
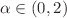, where the second one is also the generator of a strict stable process 
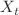of order 
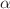with 
. The nonlinearity 
is assumed to be Lipschitz continuous. A formulation of mild random field solutions is obtained due to the called space-time fractional Green functions G, H, where H contains a singular kernel. We focus on studying the spatially–temporally Hölder continuity of mild random field solutions, which can be obtained by constructing relevant moment bounds for increments of the convolutions 
and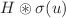 
. Our techniques are based on connecting the space-time fractional Green functions G, H to the fundamental solution of 
, 
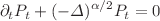via the Wright-type function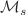 
.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2021
