Optimal rates for the parameter prediction of a Gaussian Vasicek process

Anas D. Khalaf; Anwar Zeb; Younis A. Sabawi; Salih Djilali; Xiangjun Wang

doi:10.1140/epjp/s13360-021-01738-9

EPJ

Optimal rates for the parameter prediction of a Gaussian Vasicek process

Anas D. Khalaf¹, Anwar Zeb², Younis A. Sabawi³, Salih Djilali⁴^,5^d and Xiangjun Wang¹

¹ School of Mathematics and Statistics, Huazhong University of Science and Technology, 430074, Wuhan, Hubei, People’s Republic of China
² Department of Mathematics, COMSATS University Islamabad, Abbottabad Campus, Abbottabad, Pakistan
³ Department of Mathematics, Faculty of Science and Health, Koya University, KOY45, Kurdistan Region - F. R., Koya, Iraq
⁴ Laboratoire d’Analyse Non Linéaire et Mathématiques Appliquées, Université de Tlemcen, Tlemcen, Algeria
⁵ Faculty of Exact Sciences and Informatics, Mathematic Department, Hassiba Benbouali University, Chlef, Algeria

Received: 25 May 2021
Accepted: 7 July 2021
Published online: 6 August 2021

Abstract

In this article, we deal with statistical estimation problems of drift parameters of a Vasicek-type model that is perturbed by Gaussian noise that is defined via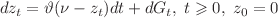

d z_{t} = ϑ (ν - z_{t}) d t + d G_{t}, t ⩾ 0, z_{0} = 0

$dz_t=\vartheta (\nu -z_t)dt+dG_t,\;t\geqslant 0, \; z_0=0$ with unknown parameters

ϑ > 0

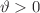$\vartheta >0$ and

ν \in R

$\nu \in {\mathbb {R}}$ , where G is a Gaussian process with index

α \in (0, 1)

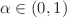$\alpha \in (0,1)$ . Based on discrete observations and using tools from Malliavin calculus together with Nordin–Peccati analysis, we provide estimators

\hat{ϑ}

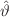${\hat{\vartheta }}$ of

ϑ

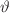$\vartheta$ and

\hat{ν}

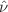${\hat{\nu }}$ of

ν

$\nu$ . Moreover, the strong consistency and asymptotic normality of our estimators have been established using the properties of G. The rates of convergence in total variation for a sequence of random variables living in a fixed Wiener chaos are computed. Finally, we discuss the case when the process G is replaced by a fractional Brownian motion.

12 Internat. Congress of the Balkan Physical Union
July 8-12, 2025
Bucharest, Romania

EPJ

Optimal rates for the parameter prediction of a Gaussian Vasicek process

Conference announcements