https://doi.org/10.1140/epjp/s13360-021-01670-y
Regular Article
Sub-bosonic (deformed) ladder operators
1
Departamento de Física, Universidade Federal de Pernambuco, 50670-901, Recife, Pernambuco, Brazil
2
Department of Physics, University of Wisconsin-Madison, 53706, Madison, WI, USA
Received:
23
March
2021
Accepted:
13
June
2021
Published online:
22
June
2021
The canonical operator 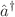 (
( ) represents the ideal process of adding (subtracting) an exact amount of energy E to (from) a physical system in both elementary quantum mechanics and quantum field theory. This is a “sharp” notion in the sense that no variability around E is possible at the operator level. In this work, we present a class of deformed creation and annihilation operators that originates from a rigorous notion of fuzziness. This leads to deformed, sub-bosonic commutation relations inducing a simple algebraic structure with modified eigenenergies and Fock states. In addition, we investigate possible consequences of the introduced formalism in quantum field theories, as for instance, deviations from linearity in the dispersion relation for free quasibosons.
) represents the ideal process of adding (subtracting) an exact amount of energy E to (from) a physical system in both elementary quantum mechanics and quantum field theory. This is a “sharp” notion in the sense that no variability around E is possible at the operator level. In this work, we present a class of deformed creation and annihilation operators that originates from a rigorous notion of fuzziness. This leads to deformed, sub-bosonic commutation relations inducing a simple algebraic structure with modified eigenenergies and Fock states. In addition, we investigate possible consequences of the introduced formalism in quantum field theories, as for instance, deviations from linearity in the dispersion relation for free quasibosons.
© The Author(s), under exclusive licence to Società Italiana di Fisica and Springer-Verlag GmbH Germany, part of Springer Nature 2021




