Eur. Phys. J. Plus (2021) 136: 461
https://doi.org/10.1140/epjp/s13360-021-01454-4

Regular Article

Modulational instability, interactions of two-component localized waves and dynamics in a semi-discrete nonlinear integrable system on a reduced two-chain lattice

¹ School of Applied Science, Beijing Information Science and Technology University, 100192, Beijing, China
² State Key Laboratory of Information Photonics and Optical Communications, and School of Science, Beijing University of Posts and Telecommunications, P. O. Box 122, 100876, Beijing, China

^b xiaoyongwen@bistu.edu.cn

Received: 30 December 2020
Accepted: 17 April 2021
Published online: 28 April 2021

Abstract

In this paper, we investigate a semi-discrete two-component integrable system on zigzag-runged ladder lattice and find a variety of two-component localized waves. First of all, we investigate the modulational instability to reveal the formation mechanism of rogue waves from three distinct plane-wave solutions for this system. Secondly, the discrete generalized 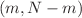-fold Darboux transformation is first constructed to solve this system. As applications, three kinds of plane-wave seed solutions are chosen to exhibit discrete two-component localized wave solutions including rogue wave solutions, breather solutions, periodic wave solutions and interaction solutions. Moreover, the dynamical behaviors of such localized wave solutions are discussed via numerical simulation. Finally, we summarize a few mathematical features to obtain various two-component localized waves through the discrete generalized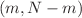-fold Darboux transformation. It is found that there are simultaneously bright–dark, dark–bright and bright–bright two-component rogue wave solutions in this discrete two-component system, and moreover, the shapes of bright–dark rogue waves in two components appear alternately with the increase of order number of Darboux transformation when some special seed solutions are selected, which have not been reported before. It is hoped that the results obtained in this paper may be used to understand some related physical phenomena.