Eur. Phys. J. Plus (2021) 136: 438
https://doi.org/10.1140/epjp/s13360-021-01436-6

Regular Article

Second-order modes of transverse oscillations in intense beams: Chernin’s matrix formalism versus Vlasov–Poisson equations

School of Particles and Accelerators, Institute for Research in Fundamental Sciences (IPM), P.O. Box 19395-5531, Tehran, Iran

^a m.aslaninejad@ipm.ir

Received: 21 January 2021
Accepted: 12 April 2021
Published online: 23 April 2021

Abstract

We study an intense space charge dominated beam in the realm of beam optics of particle accelerators. We assume an anisotropic beam with different external focussing constants and with different phase space emittances in the two transverse directions. We consider the root mean square moment equations of the beam with linear transverse coupling of particle motion ( and 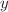). Magnetic focussing fields and the space charge Coulomb’s self-field forces are expressed in a matrix format and describe the governing equations for the beam outer envelope. By linearizing the equations, we investigate the collective response of ensemble of particles. This response is stated as coherent mode frequencies for the second-order even (envelope) and odd (tilting) oscillation modes of the beam cross section. We discuss the main features of the eigenfrequencies in detail. The approach known as Chernin’s matrix formalism is conceptually equivalent to the second-order moments of the full Vlasov–Poisson kinetic equation in four-dimensional phase space. We show that the relations obtained via matrix approach are in full agreement with the eigenfrequencies of transverse oscillations obtained by the linearized kinetic Vlasov–Poisson equations.