Eur. Phys. J. Plus (2021) 136: 358
https://doi.org/10.1140/epjp/s13360-021-01350-x

Regular Article

Symbolic computation of Caudrey–Dodd–Gibbon equation subject to periodic trigonometric and hyperbolic symmetries

¹ Department of Actuary, Faculty of Science, Firat University, 23100, Elazig, Turkey
² Department of Computer Engineering, Faculty of Engineering, Ardahan University, 75000, Ardahan, Turkey
³ Institute of Ground Water Studies, Faculty of Natural and Agricultural Sciences, University of the Free State, Bloemfontein, South Africa
⁴ Department of Basic Sciences and Related Studies, Mehran University of Engineering and Technology, Jamshoro, Pakistan

^c kashif.abro@faculty.muet.edu.pk

Received: 6 November 2020
Accepted: 23 March 2021
Published online: 4 April 2021

Abstract

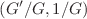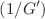The nonlinear evolution equations have been being continuously traced out to have remarkable progress and innovative applications by mathematicians and physicists. In this context, the comparison of $(G^{\prime }/G,1/G)$ and $(1/G^{\prime })$-expansion methods has been perceived for the Caudrey–Dodd–Gibbon equation on account of obtaining the periodic trigonometric, hyperbolic and rational traveling wave solutions. For the sake of advantages and disadvantages of imposed mathematical method, the standing wave with arbitrary values has been depicted in terms of contour, 3-dimension and 2-dimension graphs. The new types of periodic trigonometric, hyperbolic and rational solutions of the Caudrey–Dodd–Gibbon equation have been obtained by the comparison of both imposed methods. Additionally, solution function in the classical 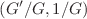$(G^{\prime }/G,1/G)$-expansion method is presented in a different form. The proposed methods for the comparison have proved to provide a powerful mathematical tool to solve nonlinear Caudrey–Dodd–Gibbon equation. By performing complicated and difficult operations via computer package program, our results showed the production of shock waves from investigated analytical solutions.